Γεωδαισιακή Καμπύλη
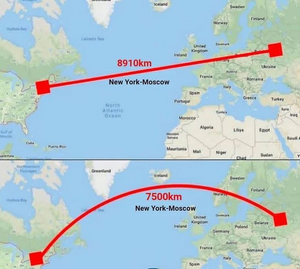
Βραχυστόχρονη Καμπύλη
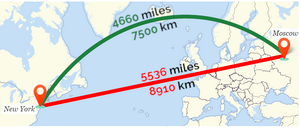
Βραχυστόχρονη Καμπύλη
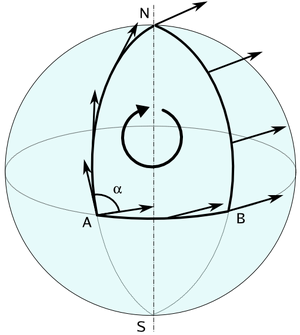
Παράλληλη Μεταφορά
If one starts from point A on the equator of a sphere and moves to the North pole, the tangent vector along the curve will look like the one shown in the figure, perpendicular to the equatorial line.
Continuing this path from the North pole, if one wishes to reach a different point B on the equator, the vector field described will have undergone a 90 degrees rotation, so the vector points along the equatorial line.
This can be easily visualised as walking to the North pole from A with your arm outstretched forward (representing the tangent vector), which is perpendicular to the equator.
Once you reach, you need to go to point B, so your body rotates, but your arm is fixed because of parallel transport, so you’re now walking with your arm outstretched to the left.
Once you reach point B, you realise that your arm is along the equatorial line.
Therefore parallel transport isn’t preserved because of the curvature of the sphere.
Since this is a property that directly results from the intrinsic curvature of the sphere, one can deduce that there is no definition of globally parallel vector fields.
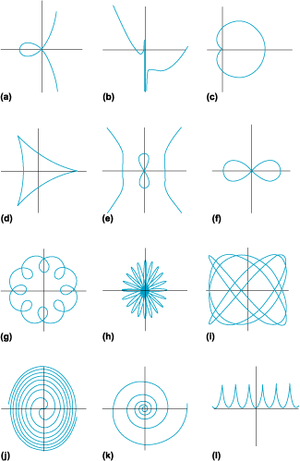
Μαθηματικά
Γεωμετρία
Καμπύλη
Καμπύλες
(a) Δεξιά Στροφοειδής Καμπύλη (Right strophoid)
(b) Τρίαινα Newton (Trident of Newton)
(c) Καρδιοειδής Καμπύλη (Cardioid)
(d) Δελτοειδής Καμπύλη (Deltoid)
(e) Δαιμονική Καμπύλη (Devil on two sticks)
(f) Λημνίσκος Bernoulli (Lemniscate of Bernoulli)
(g) Επιτροχοειδής Καμπύλη (Epitrochoid)
(h) Ροδονέα Καμπύλη (Rhodonea curve)
(i) Καμπύλη Bowditch (Bowditch curve)
(j) Σπείρα Fermat (Fermat's spiral)
(k) Λογαριθμική Σπείρα (Logarithmic spiral)
(l) Κυκλοειδής Καμπύλη (Cycloid)
- Μία καμπύλη.
- Είναι η γραμμή επάνω σε οποιαδήποτε επιφάνεια που ενώνει δύο σημεία της και έχει το ελάχιστο δυνατόν μήκος π.χ. Ο μέγιστος κύκλος στην επιφάνεια μίας σφαίρας.
- Στους μη-Ευκλείδειους χώρους, αντικαθιστά την έννοια της ευθείας
Ετυμολογία[]
Η ονομασία "Γεωδαισιακή" σχετίζεται ετυμολογικά με την λέξη "Γεωδαισία".
Ορισμοί[]
Είναι η γενίκευση της ευθείας γραμμής σε Καμπύλους Χώρους.
Είναι εκείνη η γραμμή, επάνω στην επιφάνεια που ενώνει δύο σημεία της, που έχει το ελάχιστο δυνατό μήκος. Το γνωστότερο παράδειγμα γεωδαισιακής, είναι ένας μέγιστος κύκλος στην επιφάνεια μιας σφαίρας.
Γεωδαισιακή καμπύλη είναι η καμπύλη (ή διαδρομή) με το ελάχιστο (ή μέγιστο) μήκος ανάμεσα σε δύο γειτονικά σημεία.
Με άλλη διατύπωση οι γεωδαισιακές καμπύλες μία κλάση καμπυλών σε ένα Μαθηματικό Πολύπτυχο M, μια χαρακτηριστική ιδιότητα των οποίων είναι ότι ελαχιστοποιούν την απόσταση μεταξύ δύο αρκετά γειτονικών σημείων της M.
Επιπλέον, είναι γνωστό ότι δεδομένου ενός σημείου p του Πολύπτυχου M και εφαπτόμενου διανύσματος v στο p, υπάρχει μοναδική γεωδαισιακή καμπύλη διερχόμενη από το p με κατεύθυνση το v.
A geodesic can be thought of as a curve which parallel transports its own tangent vector.
Another way of saying this is that it’s the curve of shortest distance between two points in a given space of any curvature, implying local parallel transport.
In the case of a sphere, a geodesic lies on a great circle, defined as the circle on the surface of a sphere which lies in a plane passing through the sphere’s centre.
Ανάλυση[]
Έστω x = x(s) η παραμετρική εξίσωση μιας καμπύλης που ανήκει σε ένα Πολύπτυχο.
Τότε, το διάνυσμα A = dx/ds είναι το μοναδιαίο Εφαπτομενικό Διάνυσμα της καμπύλης στο σημείο P(x).
Προφανώς, στο σημείο Q(x+dx) αντιστοιχεί το εφαπτομενικό διάνυσμα A+dA.
Αν το εφαπτομενικό διάνυσμα A υποστεί Παράλληλη Μεταφορά από το P στο Q, τότε στο Q το διάνυσμα που θα προκύψει θα είναι A+δA.
Ορίζουμε, λοιπόν, ως γεωδαισιακή την καμπύλη εκείνη για την οποία η διαφορά DA = dA-δΑ είναι μηδενική.
Δηλαδή, κατά μήκος μιας γεωδαισιακής το εφαπτόμενο διάνυσμα μετατοπίζεται παράλληλα στον εαυτό του και συνεπώς αποτελεί την άριστη («ευθεία») καμπύλη.
Ας σημειωθεί ότι σε καμπύλους χώρους, η παράλληλη μεταφορά ενός διανύσματος από ένα δεδομένο σημείο σε ένα άλλο, δίνει διαφορετικά αποτελέσματα αν πραγματοποιηθεί διαμέσου διαφορετικών καμπυλών. Δηλαδή, αν μεταφέρουμε ένα διάνυσμα παράλληλα στον εαυτό του κατά μήκος μια κλειστής διαδρομής, τότε κατά την επιστροφή του στο αρχικό σημείο δεν θα συμπίπτει, γενικά, με την αρχική του τιμή.
Ανάλυση[]
Σύμφωνα με την Γενική Θεωρία Σχετικότητας, τα σώματα (τόσο τα υλικά (π.χ. η Γη) όσο και το φως) όταν κινούνται "ελεύθερα" (δηλ. μόνον υπό την επίδραση του Βαρυτικού Πεδίου στο οποίο βρίσκονται) δεν ακολουθούν οποιεσδήποτε καμπύλες τροχιές, αλλά τις γεωδαισιακές διαδρομές του τετραδιάστατου Χωροχρόνου.
Ένα παράδειγμα γεωδαισιακής είναι η τροχιά που διαγράφει η σκιά ενός αεροπλάνου που ίπταται επάνω από λόφους. Αν και το αεροπλάνο ακολουθεί ευθεία γραμμή στον επίπεδο (flat) τρισδιάστατο χώρο, η σκιά του ακολουθεί καμπύλη γραμμή στον καμπύλο (curved) δισδιάστατο χώρο του εδάφους.
Όπως προαναφέρθηκε οι γεωδαισιακές είναι καμπύλες ελάχιστου μήκους που συνδέουν δύο σημεία του χωροχρόνου.
Οι εξισώσεις του Αϊνστάιν δίνουν τη δυνατότητα να μελετηθούν οι ιδιότητες του Χωροχρόνου σε ένα Βαρυτικό Πεδίο, (περιγράφουν δηλαδή την καμπυλότητα του Χωροχρόνου), δεν εξηγούν όμως τον τρόπο που θα κινηθούν τα σώματα σε αυτόν τον καμπύλο χώρο.
Για να αντιμετωπίσουμε αυτή τη δυσκολία, υποθέτουμε ότι τα σωμάτια και οι ακτίνες φωτός κινούνται μέσα στον χωροχρόνο με τον πιο αποτελεσματικό τρόπο.
Ακριβέστερα, αν ένα σώμα πρόκειται να κινηθεί από το σημείο Α στο σημείο Β, η τροχιά που θα ακολουθήσει θα είναι η πιο σύντομη απόσταση που συνδέει αυτά τα δύο σημεία του χωροχρόνου.
Αν ο χώρος είναι επίπεδος, είναι φανερό ότι η τροχιά θα είναι μια ευθεία γραμμή.
Αν ο χώρος είναι καμπύλος, τότε η τροχιά που θα ακολουθήσει το σώμα ονομάζεται γεωδαισιακή γραμμή.
Οι εξισώσεις που πρέπει να λυθούν για να γίνει σωστή η τροχιά που θα ακολουθήσει ένα σώμα ή μία ακτίνα φωτός ονομάζονται γεωδαισιακές εξισώσεις και πολλά προβλήματα της γενικής θεωρίας της σχετικότητας συνίστανται στην ταυτόχρονη επίλυση των εξισώσεων πεδίου και των γεωδαισιακών εξισώσεων.
Οι γεωδαισιακές καμπύλες διακρίνονται
- σε χρονοειδείς,
- φωτοειδείς
- χωροειδείς,
αν αντίστοιχα το διάνυσμα που εφάπτεται σε καθεμία από αυτές είναι χρονοειδές, φωτοειδές ή χωροειδές.
Αν δοθεί ένα σημείο του χωροχρόνου, τότε υπάρχουν άπειρες φωτοειδείς γ.γ. που περνούν από αυτό το σημείο.
Όλες οι εφαπτόμενες αυτών των φωτοειδών γ.γ. σχηματίζουν μια κωνική επιφάνεια στο σημείο αυτό του χωροχρόνου που ονομάζεται Κώνος Φωτός (light cone).
- Οι χρονοειδείς καμπύλες που διέρχονται από το δεδομένο σημείο βρίσκονται μέσα στην κωνική επιφάνεια, ενώ
- οι χωροειδείς καμπύλες που περνούν από το ίδιο σημείο βρίσκονται έξω από την κωνική επιφάνεια.
Η φυσική σημασία των καμπυλών αυτών έγκειται στην ονομαζόμενη γεωδαισιακή υπόθεση.
Σύμφωνα με αυτήν, δεχόμαστε ότι
- τα σωμάτια που κινούνται ελεύθερα (δηλαδή μόνο υπό την επίδραση του πεδίου βαρύτητας, που είναι αποτέλεσμα της καμπύλωσης του χωροχρόνου από την ύλη) ακολουθούν χρονοειδείς γ.γ., ενώ
- τα ελεύθερα φωτόνια ακολουθούν φωτοειδείς γ.γ.
Γενικότερα,
- οι χρονοειδείς καμπύλες παριστάνουν τροχιές υλικών σημείων και
- οι φωτοειδείς τροχιές φωτονίων.
Με όσα γνωρίζουμε σήμερα, κανένα υλικό σώμα δεν μπορεί να κινηθεί επι μίας χωροειδούς καμπύλης.
Υποσημειώσεις[]
Εσωτερική Αρθρογραφία[]
- Εγγενής Καμπυλότητα
- Κυκλοειδής Καμπύλη,
- Καρδιοειδής Καμπύλη,
- Νεφροειδής Καμπύλη,
- Δελτοειδής Καμπύλη,
- Αστεροειδής Καμπύλη,
- Ελικοειδής Καμπύλη,
- Κογχοειδής Καμπύλη,
Βιβλιογραφία[]
Ιστογραφία[]
- Ομώνυμο άρθρο στην Βικιπαίδεια
- Ομώνυμο άρθρο στην Livepedia
- Γεωδαισιακή Εξίσωση
- General relativity, Schurtz
- videoclip
|
Αν και θα βρείτε εξακριβωμένες πληροφορίες "Οι πληροφορίες αυτές μπορεί πρόσφατα Πρέπει να λάβετε υπ' όψη ότι Επίσης, |
- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν
- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)
