Ελαστομηχανική

Ελαστοδυναμική

Linear Elasticity , Elastic Dynamics

Φυσική

---

Φυσικοί Γης Νόμοι Φυσικής Νόμοι Φυσικής Θεωρίες Φυσικής Πειράματα Φυσικής Παράδοξα Φυσικής

Ελαστομηχανική
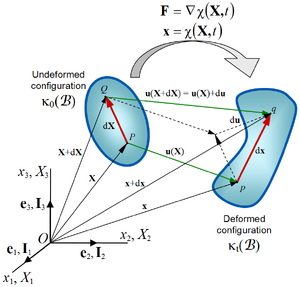
Ελαστοδυναμική
---
Ελαστικότητα
Παραμόρφωση

Ελαστικότητα
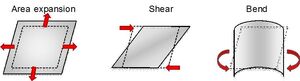
Παραμόρφωση

Ελαστικότητα
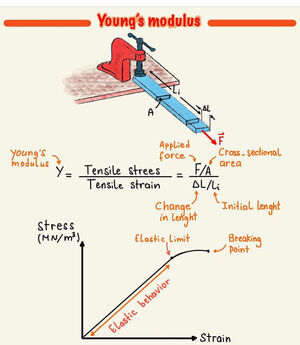
Παραμόρφωση

- Ένας Επιστημονικός Κλάδος της Μηχανικής.

Ετυμολογία

Η ονομασία "Ελαστοδυναμική" σχετίζεται ετυμολογικά με την λέξη "ελαστικότητα".

Εισαγωγή

Η Θεωρία ελαστικότητας είναι κλάδος της Μηχανικής και των Μαθηματικών που αφορά στη μοντελοποίηση της συμπεριφοράς στερεού σώματος, υπό την επίδραση εξωτερικών δράσεων (δυνάμεων και ροπών, μετατοπίσεων, θερμοκρασιακών διαφορών) όταν αυτό θεωρηθεί ως

• συνεχές,
• ομογενές,
• ισότροπο και
• ελαστικό.

Πιο συγκεκριμένα, η Θεωρία ελαστικότητας είναι κλάδος της Μηχανικής παραμορφωσίμων σωμάτων, η οποία με τη σειρά της κλάδος της Μηχανικής του συνεχούς μέσου. Η Μηχανική του συνεχούς μέσου άλλωστε περιλαμβάνει τη Μηχανική παραμορφωσίμων σωμάτων και τη Μηχανική Ρευστών.

Στη γενική περίπτωση ένα στερεό σώμα μπορεί υπό την επίδραση δυνάμεων ή άλλων δράσεων να επιταχύνεται και/ή να παραμορφώνεται. Ωστόσο αν το μοντέλο που επιλέξουμε είναι γραμμικό τότε τα δύο μπορούν να εξεταστούν ανεξάρτητα.

Άρα λοιπόν στη Θεωρία ελαστικότητας σπάνια εξετάζουμε μη-γραμμικά μοντέλα. Επίσης σπάνια εξετάζουμε μοντέλα που περιλαμβάνουν δυναμική συμπεριφορά (επιταχύνσεις).

Με άλλα λόγια μια εισαγωγή στη θεωρία ελαστικότητας κατ' αρχήν εξετάζει τις παραμορφώσεις γραμμικού ελαστικού σώματος υπό την επίδραση δυνάμεων και ροπών και εξωτερικά επιβαλλόμενων μετατοπίσεων.

Η Μηχανική παραμορφωσίμων σωμάτων έχει λοιπόν αρκετούς άλλους κλάδους όπως την Αντοχή Υλικών, τη Θεωρία πεπερασμένων στοιχείων, τη μοντελοποίηση δυναμικών αποκρίσεων, τη μοντελοποίηση παραμορφώσεων υπό την επίδραση θερμικής διαστολής/συστολής, τη θεωρία γραμμικών τέλεια πλαστικών σωμάτων και άλλους.

Ο τανυστής των τάσεων

Οι εξισώσεις των τάσεων προκύπτουν από τον δεύτερο νόμο του Νεύτωνα που είναι σε τανυστική μορφή :

$\ \sigma _{ij,j}+F_{i}=\rho \partial _{tt}u_{i}$

Για μηδενικές επιταχύνσεις έχουμε:

${\frac {\partial \sigma _{x}}{\partial x}}+{\frac {\partial \tau _{yx}}{\partial y}}+{\frac {\partial \tau _{zx}}{\partial z}}+F_{x}=0$

${\frac {\partial \tau _{xy}}{\partial x}}+{\frac {\partial \sigma _{y}}{\partial y}}+{\frac {\partial \tau _{zy}}{\partial z}}+F_{y}=0$

${\frac {\partial \tau _{xz}}{\partial x}}+{\frac {\partial \tau _{yz}}{\partial y}}+{\frac {\partial \sigma _{z}}{\partial z}}+F_{z}=0$

Πρόκειται για 3 γραμμικά ανεξάρτητες εξισώσεις με 6 αγνώστους. Η παραπάνω μορφή προκύπτει για ορθογώνιο Σύστημα Συντεταγμένων.

Ο τανυστής των τροπών

Αρχείο:Deformation-wik.jpg

Οι εξισώσεις των τροπών, δηλαδή των ανηγμένων παραμορφώσεων, προκύπτουν με χρήση διαφορικής ανάλυσης για τον στοιχειώδη κύβο όταν αυτός παραμορφωθεί. Αφορούν δηλαδή απλά τη γεωμετρία του παραμορφωμένου κύβου όταν αυτός θεωρηθεί πολύ μικρός. Ανηγμένη παραμόρφωση στη μία διάσταση σημαίνει παραμόρφωση διά το αρχικό μήκος (αδιάστατο δηλαδή μέγεθος). Στις τρεις διαστάσεις τις ονομάζουμε τροπές και γενικά λαμβάνουν πιο πολύπλοκη έκφραση:

$\epsilon _{x}={\frac {\partial u_{x}}{\partial x}}$

$\gamma _{xy}={\frac {\partial u_{x}}{\partial y}}+{\frac {\partial u_{y}}{\partial x}}$

$\epsilon _{y}={\frac {\partial u_{y}}{\partial y}}$

$\gamma _{yz}={\frac {\partial u_{y}}{\partial z}}+{\frac {\partial u_{z}}{\partial y}}$

$\epsilon _{z}={\frac {\partial u_{z}}{\partial z}}$

$\gamma _{zx}={\frac {\partial u_{z}}{\partial x}}+{\frac {\partial u_{x}}{\partial z}}$

Οι οποίες είναι 6 εξισώσεις με 9 αγνώστους. Σε τανυστική μορφή μπορούν να γραφούν:

$\varepsilon _{ij}={\frac {1}{2}}(u_{j,i}+u_{i,j})$

Οι εξισώσεις συμβιβαστότητας

Οι 6 εξισώσεις των τροπών δεν είναι ανεξάρτητες μεταξύ τους.

Απαλείφοντας τις μετατοπίσεις $u_{x}\,$, $u_{y}\,$, $u_{z}\,$ προκύπτουν οι 6 εξισώσεις συμβιβαστότητας:

${\frac {\partial ^{2}\epsilon _{x}}{\partial y^{2}}}+{\frac {\partial ^{2}\epsilon _{y}}{\partial x^{2}}}={\frac {\partial ^{2}\gamma _{xy}}{\partial x\partial y}}$

${\frac {\partial ^{2}\epsilon _{y}}{\partial z^{2}}}+{\frac {\partial ^{2}\epsilon _{z}}{\partial y^{2}}}={\frac {\partial ^{2}\gamma _{yz}}{\partial y\partial z}}$

${\frac {\partial ^{2}\epsilon _{z}}{\partial x^{2}}}+{\frac {\partial ^{2}\epsilon _{x}}{\partial z^{2}}}={\frac {\partial ^{2}\gamma _{zx}}{\partial x\partial z}}$

$2{\frac {\partial ^{2}\epsilon _{x}}{\partial y\partial z}}={\frac {\partial }{\partial x}}(-{\frac {\partial \gamma _{yz}}{\partial x}}+{\frac {\partial \gamma _{xz}}{\partial y}}+{\frac {\partial \gamma _{xy}}{\partial z}})$

$2{\frac {\partial ^{2}\epsilon _{y}}{\partial x\partial z}}={\frac {\partial }{\partial y}}(-{\frac {\partial \gamma _{xz}}{\partial y}}+{\frac {\partial \gamma _{xy}}{\partial z}}+{\frac {\partial \gamma _{yz}}{\partial x}})$

$2{\frac {\partial ^{2}\epsilon _{z}}{\partial x\partial y}}={\frac {\partial }{\partial z}}(-{\frac {\partial \gamma _{xy}}{\partial z}}+{\frac {\partial \gamma _{yz}}{\partial x}}+{\frac {\partial \gamma _{xz}}{\partial y}})$

Όταν ικανοποιούνται οι συνθήκες συμβιβαστότητας των παραμορφώσεων εξασφαλίζεται η ύπαρξη μονοσήμαντου και συνεχούς πεδίου τιμών για την ανηγμένη παραμόρφωση.

Γραμμική ελαστικότητα

Για τον προσδιορισμό των έξι παραμορφώσεων διαθέτουμε τρεις διαφορικές εξισώσεις. Άρα το πρόβλημα είναι τρεις φορές αόριστο. Για τον προσδιορισμό των έξι ανηγμένων παραμορφώσεων και των τριών μετατοπίσεων διαθέτουμε έξι διαφορικές εξισώσεις. Πάλι λείπουν τρεις σχέσεις. Συνολικά δεκαπέντε άγνωστοι και εννέα εξισώσεις. Η αοριστία μπορεί να αρθεί αν εισάγουμε τις λεγόμενες καταστατικές εξισώσεις για το υλικό.

Στην περίπτωση γραμμικά ελαστικού, ομογενούς και ισότροπου υλικού ο νόμος του Hooke στις τρεις διαστάσεις γράφεται:

$\epsilon _{x}={\frac {1}{E}}[\sigma _{x}-\nu (\sigma _{y}+\sigma _{z})]+\alpha \Delta T$

$\epsilon _{y}={\frac {1}{E}}[\sigma _{y}-\nu (\sigma _{x}+\sigma _{z})]+\alpha \Delta T$

$\epsilon _{z}={\frac {1}{E}}[\sigma _{z}-\nu (\sigma _{x}+\sigma _{y})]+\alpha \Delta T$

$\gamma _{xy}={\frac {1}{G}}\tau _{xy}$

$\gamma _{xz}={\frac {1}{G}}\tau _{xz}$

$\gamma _{yz}={\frac {1}{G}}\tau _{yz}$

Σύμβολα που χρησιμοποιήθηκαν

• $\sigma \,$ είναι η ορθή τάση
• $\tau \,$ είναι η διατμητική τάση
• $F\,$ είναι οι δυνάμεις σώματος
• $\epsilon\,$ είναι η ορθή ανηγμένη παραμόρφωση (τροπή)
• $\gamma \,$ είναι η διατμητική ανηγμένη παραμόρφωση (τροπή)
• $\ E$, $\ G$, $\ \nu$ και $\ \alpha$ το μέτρο ελαστικότητας, το μέτρο ελαστικότητας σε διάτμηση, ο λόγος του Poisson και ο συντελεστής θερμικής διαστολής αντίστοιχα είναι ιδιότητες του υλικού
• $\ \Delta T$ είναι η θερμοκρασιακή μεταβολή.

Αριθμητική Επίλυση

Η μορφή που παίρνει το μοντέλο ώστε να είναι επιλύσιμο με τη μέθοδο των πεπερασμένων στοιχείων αλλάζει (μετασχηματίζεται) σε σχέση με το αρχικό μοντέλο. Πολλές αριθμητικές μέθοδοι μπορούν να χρησιμοποιηθούν και η επιλογή μπορεί να εξαρτάται απ'τις συνοριακές συνθήκες, τη γεωμετρία του συγκεκριμένου προβλήματος που εξετάζεται, απ'το αν υπάρχει ήδη διαθέσιμος κώδικας και από άλλους τεχνικούς παράγοντες.

Ακριβής Επίλυση

Ακριβής επίλυση είναι δυνατή μόνο σε πολύ συγκεκριμένες περιπτώσεις προβλημάτων, κατά κανόνα με μείωση των διαστάσεων σε μία, και συγκεκριμένες συνοριακές συνθήκες. Ιστορικά η ακριβής επίλυση προηγήθηκε και αποτελεί τον κλάδο της Αντοχής των Υλικών.

Εσωτερική Αρθρογραφία

• Ελαστικότητα
• Πλαστικότητα
• Αντοχή Υλικών
• Τεχνική Μηχανική

Βιβλιογραφία

• Theory and Problems of Strength of Materials, W. A. Nash, 1977
• Μηχανική Παραμορφωσίμων Σωμάτων Ι, Γ.Ι. Τσαμασφύρος, 1991

Ιστογραφία

• Ομώνυμο άρθρο στην Βικιπαίδεια
• Ομώνυμο άρθρο στην Livepedia
• [ ]
• [ ]

Κίνδυνοι Χρήσης

Αν και θα βρείτε εξακριβωμένες πληροφορίες σε αυτήν την εγκυκλοπαίδεια ωστόσο, παρακαλούμε να λάβετε σοβαρά υπ' όψη ότι η "Sciencepedia" δεν μπορεί να εγγυηθεί, από καμιά άποψη, την εγκυρότητα των πληροφοριών που περιλαμβάνει. "Οι πληροφορίες αυτές μπορεί πρόσφατα να έχουν αλλοιωθεί, βανδαλισθεί ή μεταβληθεί από κάποιο άτομο, η άποψη του οποίου δεν συνάδει με το "επίπεδο γνώσης" του ιδιαίτερου γνωστικού τομέα που σας ενδιαφέρει." Πρέπει να λάβετε υπ' όψη ότι όλα τα άρθρα μπορεί να είναι ακριβή, γενικώς, και για μακρά χρονική περίοδο, αλλά να υποστούν κάποιο βανδαλισμό ή ακατάλληλη επεξεργασία, ελάχιστο χρονικό διάστημα, πριν τα δείτε. Επίσης, Οι διάφοροι "Εξωτερικοί Σύνδεσμοι (Links)" (όχι μόνον, της Sciencepedia αλλά και κάθε διαδικτυακού ιστότοπου (ή αλλιώς site)), αν και άκρως απαραίτητοι, είναι αδύνατον να ελεγχθούν (λόγω της ρευστής φύσης του Web), και επομένως είναι ενδεχόμενο να οδηγήσουν σε παραπλανητικό, κακόβουλο ή άσεμνο περιεχόμενο. Ο αναγνώστης πρέπει να είναι εξαιρετικά προσεκτικός όταν τους χρησιμοποιεί.

- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν

---

>>Διαμαρτυρία προς την wikia<<

- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)

---