Καμπύλη
Μαθηματική Καμπύλη

καμπύλη
καμπύλη
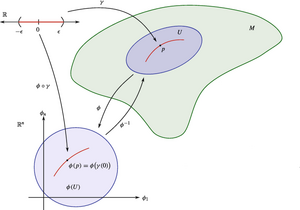
Τοπολογικός Χάρτης
Μαθηματική Καμπύλη
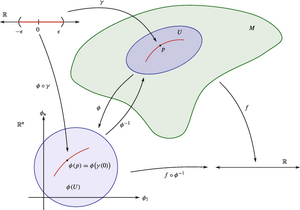
Τοπολογικός Χάρτης
Μαθηματική Καμπύλη

Χωρόχρονος
Χώρος
Χρόνος
Διάσταση
Μήκος
Πλάτος
Ύψος
Εμβαδό
Όγκος
Υπερεμβαδό
Σημείο
Καμπύλη
Επιφάνεια
Χωροπεριοχή
Κοσμικό Σημείο
Κοσμική Καμπύλη
Βράνη
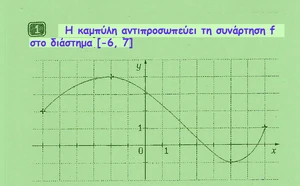
Καμπύλη

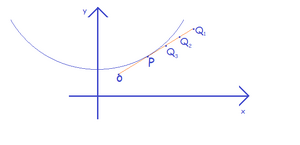
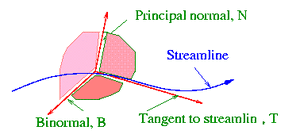
Μοναδιαίο Διάνυσμα
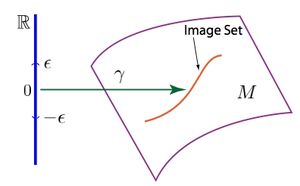
Συνάρτηση
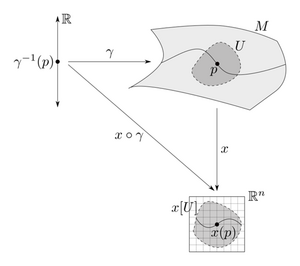
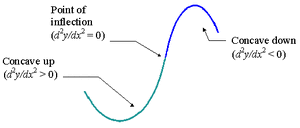
Συνάρτηση

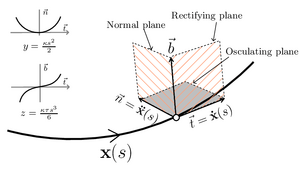
Ανορθωτικό (rectifying) Επίπεδο
Κάθετο (normal) Επίπεδο
- Ένα Γεωμετρικό Σχήμα.
Ετυμολογία[]
Η ονομασία "Καμπύλη" σχετίζεται ετυμολογικά με την λέξη "καμπή".
Εισαγωγή[]
Ως Καμπύλη γραμμή στη Γεωμετρία χαρακτηρίζεται οποιαδήποτε γραμμή της οποίας κανένα τμήμα της δεν είναι ευθύγραμμο.
Επίσης ορίζεται και ως γραμμή που μεταβάλλει κατεύθυνση χωρίς να σχηματίζει καμία γωνία.
- Κάθε επιμέρους τμήμα μιας καμπύλης λέγεται καμπύλο τμήμα ή τόξο της καμπύλης.
- Μια καμπύλη γραμμή λέγεται κλειστή όταν τα άκρα της συμπίπτουν. Το αντίθετο λέγεται ανοικτή.
Επίσης τόσο στη γεωμετρία όσο και στη φυσική ως καμπύλη ορίζεται η γραμμή που παριστά τις διαδοχικές θέσεις ενός σημείου που κινείται, όχι ευθύγραμμα, σύμφωνα με κάποιο καθορισμένο νόμο.
Έτσι η περιφέρεια κύκλου είναι κλειστή καμπύλη της οποίας όλα τα σημεία απέχουν ίση απόσταση από κάποιο άλλο εκτός σημείο (κέντρο).
Στις γραφικές παραστάσεις η καμπύλη παριστά μεταβολές κατάστασης ή εκφράζει νόμους ενός φαινομένου (συντεταγμένες), π.χ. βαρομετρική καμπύλη, μεταβολής θερμοκρασίας κ.λ.π).
Στην αρχαία ελληνική υπονοώντας τη λέξη βακτηρία ως "καμπύλες" χαρακτηρίζονταν οι ράβδοι που κρατούσαν οι χωρικοί, οι ζητιάνοι, οι ταξιδιώτες, οι παιδαγωγοί κ.λπ σε αντίθεση με τους πλούσιους που κρατούσαν τις "ορθές" (βακτηρίες).
Κλειστή καμπύλη[]
Στη γεωμετρία, μία καμπύλη λέγεται κλειστή όταν δεν έχει άκρα και μη κλειστή ή ανοικτή στην αντίθετη περίπτωση.
Στην ευκλείδεια γεωμετρία, ο κύκλος είναι μία κλειστή καμπύλη αξιωματικά.
Κλειστή καμπύλη είναι επίσης κάθε ευθεία, από την στιγμή που δεν έχει άκρα, γεγονός που δικαιολογείται και διαισθητικά, αν θεωρήσουμε την ευθεία ως "κύκλο άπειρης ακτίνας".
Ωστόσο μία ημιευθεία δεν είναι κλειστή εφόσον έχει άκρο.
Ένας κάπως πιο αυστηρός ορισμός της κλειστής καμπύλης θα περιλάμβανε τα άκρα. Δηλαδή στην κλειστή τα δύο άκρα συμπίπτουν στο ίδιο σημείο, στην ανοικτή τα δύο άκρα είναι διαφορετικά σημεία.
Ταξινομία[]
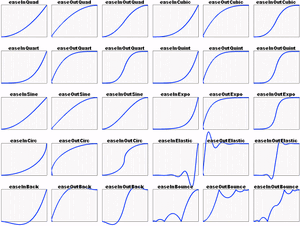
Είδη καμπυλών:
- Κυκλοειδής Καμπύλη,
- Καρδιοειδής Καμπύλη,
- Νεφροειδής Καμπύλη,
- Δελτοειδής Καμπύλη,
- Αστεροειδής Καμπύλη,
- Ελικοειδής Καμπύλη,
- Κογχοειδής Καμπύλη,
Τοπολογικός Ορισμός[]
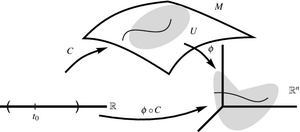
In general, a curve is defined through a continuous function from an interval of the real numbers into a topological space X. Depending on the context, it is either or its image which is called a curve.
In general topology, when non-differentiable functions are considered, it is the map , which is called a curve, because its image may look very differently from what is commonly called a curve. For example, the image of the Peano curve completely fills the square. On the other hand, when one considers curves defined by a differentiable function (or, at least, a piecewise differentiable function), this is commonly the image of the function which is called a curve.
- The curve is said to be simple, or a Jordan arc, if is injective, i.e. if for all , in , we have implies . If is a closed bounded interval , we also allow the possibility (this convention makes it possible to talk about "closed" simple curves, see below). In other words, this curve "does not cross itself and has no missing points".[1]
- If for some (other than the extremities of ), then is called a double (or multiple) point of the curve. This is a special case of a singular point of a curve.
- A curve is said to be closed or a loop if and if . A closed curve is thus the image of a continuous mapping of the circle ; a simple closed curve is also called a Jordan curve. The Jordan curve theorem states that such curves divide the plane into an "interior" and an "exterior".
Space curve[]
A plane curve is a curve for which is the Euclidean plane—these are the examples first encountered—or in some cases the projective plane. A space curve is a curve for which is of three dimensions, usually Euclidean space; a skew curve is a space curve which lies in no plane. These definitions of plane, space and skew curves apply also to real algebraic curves, although the above definition of a curve does not applies (a real algebraic curve may be disconnected).
This definition of curve captures our intuitive notion of a curve as a connected, continuous geometric figure that is "like" a line, without thickness and drawn without interruption, although it also includes figures that can hardly be called curves in common usage. For example, the image of a curve can cover a square in the plane (space-filling curve). The image of simple plane curve can have Hausdorff dimension bigger than one (see Koch snowflake) and even positive Lebesgue measure[2] (the last example can be obtained by small variation of the Peano curve construction). The dragon curve is another unusual example.
Υποσημειώσεις[]
- ↑ Jordan arc definition at Dictionary.com. Dictionary.com Unabridged. Random House, Inc. Dictionary.reference.com. http://dictionary.reference.com/browse/jordan%20arc. Ανακτήθηκε την 2012-03-14.
- ↑ Osgood, William F. (January 1903). "A Jordan Curve of Positive Area". Transactions of the American Mathematical Society (American Mathematical Society) 4 (1): 107–112. doi:. ISSN 0002-9947.
Εσωτερική Αρθρογραφία[]
Βιβλιογραφία[]
- Νεώτερο Εγκυκλοπαιδικό Λεξικό Ηλίου τομ.10ος σ.176
Ιστογραφία[]
- Ομώνυμο άρθρο στην Βικιπαίδεια
- Ομώνυμο άρθρο στην Livepedia
- upatras.gr Spirou
- Καμπύλες στο επίπεδο και στο χώρο
- Ν. Καδιανάκη, "Διαφορική Γεωμετρία Καμπυλών και επιφανειών"
|
Αν και θα βρείτε εξακριβωμένες πληροφορίες "Οι πληροφορίες αυτές μπορεί πρόσφατα Πρέπει να λάβετε υπ' όψη ότι Επίσης, |
- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν
- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)








![{\displaystyle [a,b]}](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/f6257fd8e02b31abfa0fbeed7ab806e5d09a72d6)



![{\displaystyle I=[a,b]}](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/4f3a4ad9a7e560e59bc4c6e4b72e401a46de2828)


