Μαγνητικόν Πεδίον
- Για την πλήρη μαθηματική περιγραφή του Μαγνητικού πεδίου βλέπε: Μαγνητικό Πεδίο \Οντότητα.

Ηλεκτροφυσικός Νόμος Σύνδεσης
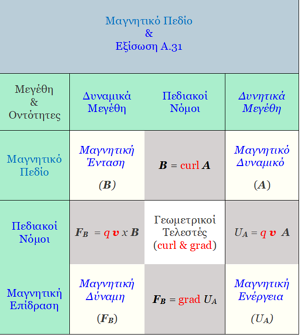

Εξίσωση A.31
Πεδίο Φυσικό Πεδίο Κλασσικό Πεδίο Κβαντικό Πεδίο Βαρυτικό Πεδίο Ηλεκτρικό Πεδίο Μαγνητικό Πεδίο Ηλεκτρομαγνητικό Πεδίο Ασθενές Πεδίο Ηλεκτρασθενές Πεδίο Χρωμικό Πεδίο Ενιαίο Πεδίο
Ομογενές Πεδίο Κεντρικό Πεδίο Σωληνοειδές Πεδίο Συντηρητικό Πεδίο
Μαθηματικό Πεδίο Βαθμωτό Πεδίο Ανυσματικό Πεδίο Τανυστικό Πεδίο


Θεώρημα Στροβιλισμού
Πεδιακός Νόμος Μαγνητικού Πεδίου (3D)
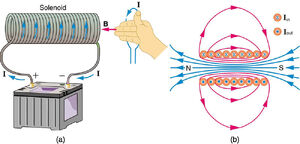
Ηλεκτρομαγνήτης Μαγνητικό Πεδίο
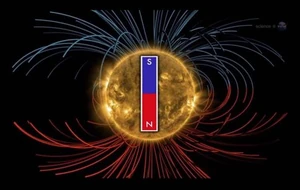
- Μία Φυσική Οντότητα αλλά και κλάδος του Ηλεκτρομαγνητισμού.
Ορισμός[]
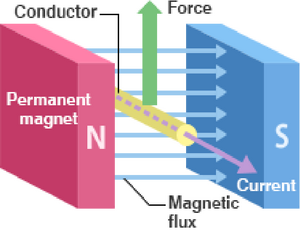
Είναι ο χώρος μέσα στον οποίο ασκούνται μαγνητικές επιδράσεις σε κινούμενα φορτισμένα σώματα ή ισοδύναμα, σε ήλεκτρικά ρεύματα.
ΣΗΜΕΙΩΣΗ: Ο χώρος αυτός δεν είναι κενός αλλά καταλαμβάνεται από ένα "νέφος" φωτονίων.
Παραδείγματα[]
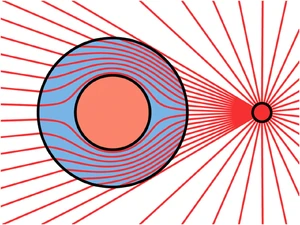
- π.χ. ο χώρος γύρω από έναν μαγνήτη.
- π.χ. ο χώρος γύρω από έναν ρευματοφόρο αγωγό (καλώδιο).
- π.χ. ο χώρος μέσα σε ένα πηνίο.
Φυσικά Μεγέθη Μαγνητικού Πεδίου[]
Το Μαγνητικό Πεδίο χαρακτηρίζεται από τέσσερα φυσικά μεγέθη:
α) Τα δύο πρώτα μεγέθη χαρακτηρίζονται ως δυναμικά (dynamical) και εκφράζουν την ικανότητα του Μαγνητικού Πεδίου να "επιδρά σε" κινούμενα σώματα (π.χ. ηλεκτρόνια) που βρίσκονται στον χώρο του και συνιστούν Ηλεκτρικό Ρεύμα.
Το ένα μέγεθος είναι εντατικό και το άλλο εκτατικό.
- Μαγνητική Ένταση ( B )
- Magnetic Strength
- ή Ένταση του Μαγνητικού Πεδίου
- ή παλαιότερα, Μαγνητική Επαγωγή
- Μαγνητική Ροή ( ΦB )
- Magnetic Flux
β) Τα δύο επόμενα μεγέθη χαρακτηρίζονται ως δυνητικά (potential) και εκφράζουν την δυνατότητα του Μαγνητικού Πεδίου να "παράγεται από" κινούμενα σώματα (π.χ. ηλεκτρόνια) που βρίσκονται σε ένα χώρο και συνιστούν Ηλεκτρικό Ρεύμα.
Και πάλι, το ένα μέγεθος είναι εντατικό και το άλλο εκτατικό.
- Μαγνητικό Δυναμικό ( A )
- Magnetic Potential
- ή Δυναμικό του Μαγνητικού Πεδίου
- Μαγνητική Κυκλοφορία ( ΓA )
- Magnetic Circulation
- ή ορθότερα, Μαγνητική Ρύση
- Magnetic Flow
Πεδιακός Νόμος Μαγνητικού Πεδίου[]
Τυπική Διατύπωση[]
Τα τέσσερα φυσικά μεγέθη του Μαγνητικού Πεδίου συνδέονται μεταξύ τους, ανά δύο, με τέσσερεις μαθηματικές σχέσεις.
Σχέση Εντατικών μεγεθών[]
Η Μαγνητική Ένταση (B) του Μαγνητικού Πεδίου, σε κάθε σημείο του χώρου που αυτό κατέχει,
ισούται με
τον στροβιλισμό (curl) του Μαγνητικού Δυναμικού (A) του Ηλεκτρικού Ρεύματος από το οποίο παράγεται.
- B = curl A
Σχέση Δυναμικών μεγεθών[]
Η Μαγνητική Ροή ( ΦB ) του Μαγνητικού Πεδίου, που διέρχεται από μία επιφάνεια του χώρου που αυτό κατέχει,
ισούται με
το επιφανειακό ολοκλήρωμα ( ∫∫ dΣ ) της Μαγνητικής Έντασης (B) του Μαγνητικού Πεδίου αυτού, σε κάθε σημείο της επιφάνειας αυτής.
- ΦB = ∫∫ dΣ ∙ Β
Σχέση Δυνητικών μεγεθών[]
Η Μαγνητική Ρύση ( ΓΑ ) του Ηλεκτρικού Ρεύματος, που διαρρέει έναν ρευματοφόρο αγωγό, σε ολόκληρο το μήκος του
ισούται με
το επικαμπύλιο ολοκλήρωμα ( ∫ dr ) του Μαγνητικού Δυναμικού ( A ) του Ηλεκτρικού Ρεύματος αυτού, σε κάθε σημείο του αγωγού αυτού.
- ΓA = ∫ dr ∙ A
Σχέση Εκτατικών μεγεθών[]
Η Μαγνητική Ροή ( ΦB ) του Μαγνητικού Πεδίου, που διέρχεται από μία επιφάνεια του χώρου που αυτό κατέχει,
ισούται με
την άθροιση ( Σ )
της Μαγνητικής Ρύσης ( ΓΑ ) του Ηλεκτρικού Ρεύματος, που διαρρέει έναν ρευματοφόρο αγωγό, ο οποίος περικλείει την επιφάνεια αυτή.
- ΦB = Σ ∙ ΓA
Μαθηματική Αναπαράσταση[]
| Διαφορική μορφή Πεδιακών Εξισώσεων Μαγνητικού Πεδίου | ||
|---|---|---|
| Μορφή | Συνοπτική μορφή | Αναλυτική μορφή |
| Τελεστική Αναπαράσταση |
| |
| Ανυσματική Αναπαράσταση | ||
| Τανυσματική Αναπαράσταση | ||
Συμβολισμός:
| ||
| Σχέσεις Σύνδεσης Μαγνητικού Πεδίου | ||
|---|---|---|
| Σχέση | Συνοπτική μορφή | Αναλυτική μορφή |
| Μεταξύ δυναμικών μεγεθών |
| |
| Μεταξύ δυνητικών μεγεθών |
| |
Συμβολισμός:
| ||
| Ολοκληρωτική μορφή Πεδιακών Εξισώσεων Μαγνητικού Πεδίου | ||
|---|---|---|
| Μορφή | Συνοπτική μορφή | |
| Τελεστική Αναπαράσταση | ||
| Ανυσματική Αναπαράσταση | ||
| Τανυσματική Αναπαράσταση | ||
| Μορφή | Αναλυτική μορφή | |
| Συνήθης Αναπαράσταση |
= + | |
Συμβολισμός:
| ||
Δομή Μαγνητικού Πεδίου[]
Οι Νόμοι που αφορούν το Μαγνητικό Πεδίο μπορούν να αποδοθούν κομψά από τους ακόλουθους πίνακες.
| Μαγνητικό Πεδίο (B) <Πίνακας 1> (Σύνδεση Αναπαραστάσεων μεταξύ Δυναμικών Μεγεθών) | |||
|---|---|---|---|
| -/- | Εντατικά Μεγέθη | Συνδετικοί Νόμοι | Εκτατικά Μεγέθη |
| Μαγνητικό Πεδίο | Μαγνητική Ένταση |
(Eq. 01) |
Μαγνητική Ροή |
| - | Τελεστής: Ανοικτό Επιφανειακό Ολοκλήρωμα | ||
| Μαγνητική Επίδραση | Μαγνητική Δύναμη |
(Eq. 02) |
Μαγνητικό Έργο |
| Μαγνητικό Πεδίο (B) <Πίνακας 2> (Σύνδεση Αναπαραστάσεων μεταξύ Δυνητικών Μεγεθών) | |||
|---|---|---|---|
| -/- | Εντατικά Μεγέθη | Συνδετικοί Νόμοι | Εκτατικά Μεγέθη |
| Μαγνητικό Πεδίο | Μαγνητικό Δυναμικό |
(Eq. 03) |
Μαγνητική Ρύση |
| - | Τελεστής: Ανοικτό Επικαμπύλιο Ολοκλήρωμα | ||
| Μαγνητική Επίδραση | Μαγνητική Έγερση |
(Eq. 04) |
Μαγνητική Ενέργεια |
| Μαγνητικό Πεδίο (B) <Πίνακας 3> (Εντατική Αναπαράσταση) | |||
|---|---|---|---|
| -/- | Δυναμικά Μεγέθη | Πεδιακοί Νόμοι | Δυνητικά Μεγέθη |
| Μαγνητικό Πεδίο | Μαγνητική Ένταση |
(Eq. 05) |
Μαγνητικό Δυναμικό |
| Διαδραστικοί Νόμοι | (Eq. 06) |
Τελεστής: Στροβίλιση ή |
(Eq. 07) |
| Μαγνητική Επίδραση | Μαγνητική Δύναμη |
(Eq. 08) |
Μαγνητική Έγερση |
| Μαγνητικό Πεδίο (B) <Πίνακας 4> (Εκτατική Αναπαράσταση) | |||
|---|---|---|---|
| -/- | Δυναμικά Μεγέθη | Πεδιακοί Νόμοι | Δυνητικά Μεγέθη |
| Μαγνητικό Πεδίο | Μαγνητική Ροή |
(Eq. 09) |
Μαγνητική Ρύση |
| Διαδραστικοί Νόμοι | (Eq. 10) |
Τελεστής: Διαφορά |
(Eq. 11) |
| Μαγνητική Επίδραση | Μαγνητικό Έργο |
(Eq. 12) |
Μαγνητική Ενέργεια |
| Μαγνητικό Πεδίο (B) <Πίνακας 5> (Εντατική Αναπαράσταση) | |||
|---|---|---|---|
| -/- | Εντατικά Μεγέθη | Δομικοί Νόμοι | |
| Μαγνητικό Πεδίο | Μαγνητική Ένταση |
(Eq. 13) | |
| - | Τελεστής: Στροβίλιση ή | ||
| Μαγνητική Επίδραση | Μαγνητική Δύναμη |
(Eq. 14) | |
| Μαγνητικό Πεδίο (B) <Πίνακας 6a> (Σύνδεση Αναπαραστάσεων) | |||
|---|---|---|---|
| -/- | Εντατικά Μεγέθη | Δομικοί Νόμοι | |
| Μαγνητικό Πεδίο | Μαγνητική Ένταση |
(Eq. 15) | |
| - | Τελεστής: Κλειστό Επιφανειακό Ολοκλήρωμα | ||
| Μαγνητική Επίδραση | Μαγνητική Δύναμη |
(Eq. 16) | |
| Μαγνητικό Πεδίο (B) <Πίνακας 6b> (Εκτατική Αναπαράσταση) | |||
|---|---|---|---|
| -/- | Εντατικά Μεγέθη | Δομικοί Νόμοι | |
| Μαγνητικό Πεδίο | Μαγνητική Ροή |
(Eq. 17) | |
| - | Τελεστής: Άθροισμα | ||
| Μαγνητική Επίδραση | Μαγνητικό Έργο |
(Eq. 18) | |
Υποσημειώσεις[]
Εσωτερική Αρθρογραφία[]
- Γεωμαγνητικό Πεδίο (ειδικά, Γαιομαγνητικό Πεδίο)
- Αστρομαγνητικό Πεδίο (ειδικά, Ηλιομαγνητικό Πεδίο)
- Γαλαξιακό Μαγνητικό Πεδίο
- Ηλεκτρικό Φορτίο
- Ηλεκτρικό Ρεύμα
- Ηλεκτρικό Πεδίο
- Μαγνητικό Πεδίο
Βιβλιογραφία[]
Ιστογραφία[]
|
Αν και θα βρείτε εξακριβωμένες πληροφορίες "Οι πληροφορίες αυτές μπορεί πρόσφατα Πρέπει να λάβετε υπ' όψη ότι Επίσης, |
- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν
- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)































































