Παραβολή
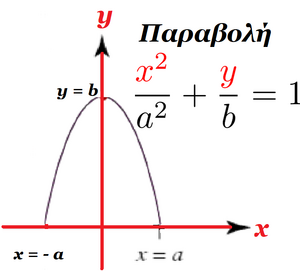
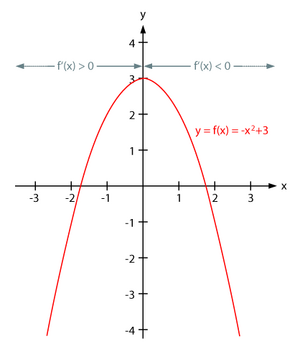
Η τυπική εξίσωσή της είναι:
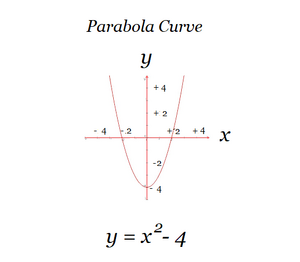
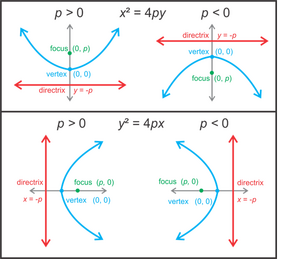
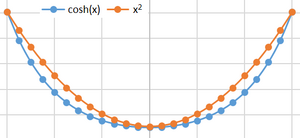
Υπερβολικό Συνημίτονο
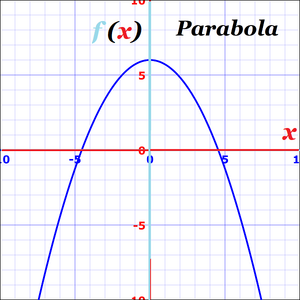




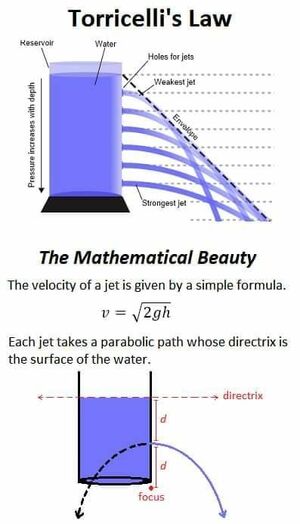
Παραβολή
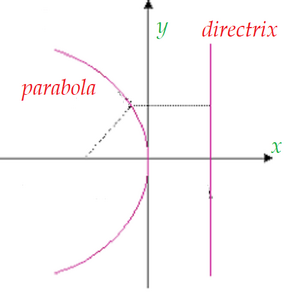
Διευθέτουσα
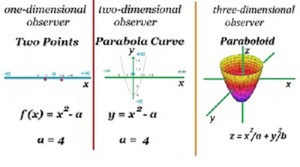
Διαστατικός Παρατηρητής
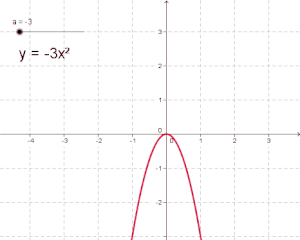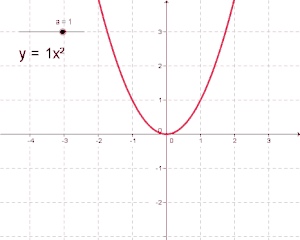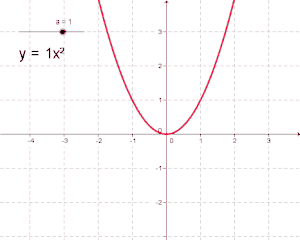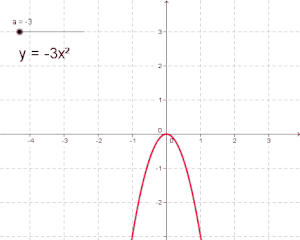
- Μία θεμελιώδης καμπύλη και ειδικότερα μία Κωνική Τομή
Ετυμολογία[]
Η ονομασία "Παραβολή" σχετίζεται ετυμολογικά με την λέξη "βολή".
Εισαγωγή[]
Στη Γεωμετρία παραβολή ονομάζεται η επίπεδη καμπύλη που προκύπτει από την τομή κώνου εκ περιστροφής επιπέδου παράλληλου προς επίπεδο εφαπτόμενο αυτού.
Βασικές Έννοιες[]
Η παραβολή μπορεί να θεωρηθεί και ως ο γεωμετρικός τόπος των σημείων ενός επιπέδου Π που ισαπέχουν από σημείου Ε (εντός καμπύλης) και ευθείας δ εκτός καμπύλης.
Συμβολικά .
Τόσο το Ε όσο και η δ κείνται επί του Π, ενώ το Ε δεν θα κείται επί της δ. Τότε το Ε καλείται εστία της παραβολής και η δ διευθετούσα της παραβολής.
Είναι προφανές πως η παραβολή είναι συμμετρική ως προς την ευθεία α, καλούμενη άξονας της παραβολής, επί της οποίας βρίσκεται το σημείο Ε και που είναι κάθετος στη διευθετούσα.
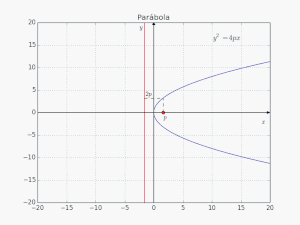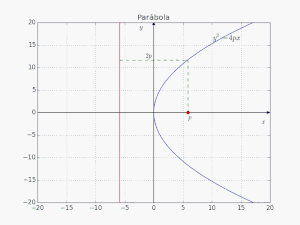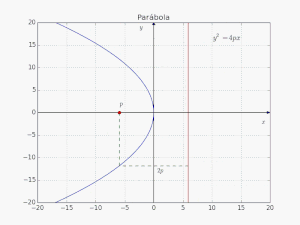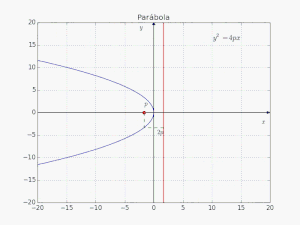
Έστω 2p η απόσταση μεταξύ της διευθετούσας και της εστίας. Θεωρούμε το σημείο τομής Β της διευθετούσας και του άξονα της παραβολής. Το μήκος του ευθήγραμμου τμήματος ΒΕ είναι προφανώς 2p. Το μέσο Α του ΒΕ ονομάζεται κορυφή της παραβολής. Το Α ισαπέχει από τη διευθετούσα και την εστία με απόσταση p.
Εξισώσεις της Παραβολής[]
Κανονική μορφή[]
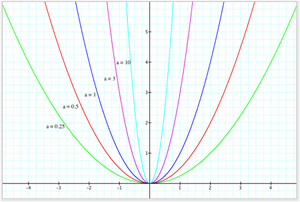
Μία παραβολή θεωρείται στην κανονική της μορφή, όταν η κορυφή της είναι στο (0,0) του συστήματος συντεταγμένων και ο άξονάς της συμπίπτει με τον άξονα τετμημένων του συστήματος συντεταγμένων.
Σε Καρτεσιανές Συντεταγμένες εκφράζεται ως:
Γενική μορφή[]
Έστω μία κωνική τομή
Η καμπύλη αυτή είναι παραβολή, αν και τουλάχιστον ένα των a, c είναι διάφορο του μηδενός.
Τυπική Μορφή[]
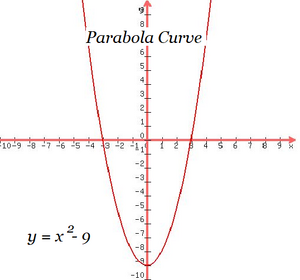
- Παραβολή (τύπος Α). Η παραβολή αυτή τέμνει τον άξονα x σε δύο σημεία και τον άξονα y σε ένα.
- Παραβολή (τύπος Β). Η παραβολή αυτή δεν τέμνει τον άξονα x ενώ τέμνει τον άξονα y σε ένα σημείο.
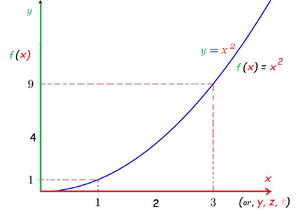
- Παραβολή (τύπος Γ). Η παραβολή αυτή διέρχεται από την αρχή των αξόνων.
Δευτεοβάθμια Αλγεβρική Συνάρτηση[]
Υποσημειώσεις[]
Εσωτερική Αρθρογραφία[]
Βιβλιογραφία[]
Ιστογραφία[]
|
Αν και θα βρείτε εξακριβωμένες πληροφορίες "Οι πληροφορίες αυτές μπορεί πρόσφατα Πρέπει να λάβετε υπ' όψη ότι Επίσης, |
- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν
- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)









