Κομβοθεωρία




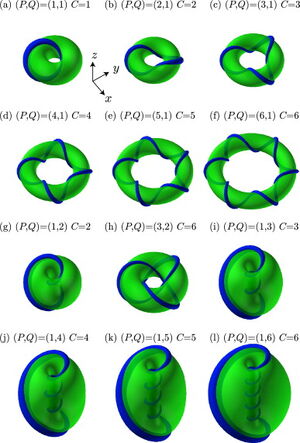
(transparent green surface) and
kink soliton string
(blue surface)
The Hopf charge C is
1 in (a),
2 in (b) and (g),
3 in (c) and (i),
4 in (d) and (j),
5 in (e) and (k),
6 in (f), (h), and (l)
- Ένας Επιστημονικός Κλάδος των Μαθηματικών.
Ετυμολογία[]
Η ονομασία "Θεωρία κόμβων" σχετίζεται ετυμολογικά με την λέξη "κόμβος".
Εισαγωγή[]
Η Θεωρία Κόμβων είναι ένας κλάδος της Τοπολογίας που εξετάζει τους κόμβους και τους κρίκους.
Στην Τοπολογία, μια σφαίρα είναι όμοια με έναν κύβο. Η Τοπολογία δεν εξετάζει τις γεωμετρικές ιδιότητες των αντικειμένων, όπως το μήκος και τις γωνίες, αλλά τις ιδιότητες οι οποίες μένουν αναλλοίωτες ως προς την αλλαγή καμπυλότητας, στρέψης και ως προς τις ελαστικές παραμορφώσεις.
Ο απλούστερος κόμβος είναι ο τετριμμένος. Ο αμέσως επόμενος είναι ο κόμβος trefoil και η κατοπτρική του εικόνα, και μετά είναι ο κόμβος figure-8. Η κατοπτρική εικόνα ενός κόμβου, είναι ο ίδιος κόμβος με αντίθετες διασταυρώσεις.
Σε όλη την ιστορία της Θεωρίας Κόμβων οι ερευνητές διατήρησαν ζωντανή τη θεωρία, βρίσκοντας διάφορες χρήσεις της. Από την Ατομική Θεωρία που προτάθηκε από το λόρδο Kelvin μέχρι την ανακάλυψη ενός μορίου DNA υπό τη μορφή κόμβου trefoil, υπήρξε πάντα ένας σκοπός και μια έμπνευση για τη Θεωρία Κόμβων. Οι εφαρμογές της σήμερα εκτείνονται από τη Στατιστική Μηχανική έως τη Χημεία και τη Μοριακή Βιολογία.
Ισοτοπία στο Χώρο[]
Ένας κόμβος είναι μια κλειστή, μονοδιάστατη και συνεχής μη τεμνόμενη καμπύλη στον τρισδιάστατο Χώρο.
Από μια πιο μαθηματική σκοπιά, ένας κόμβος είναι η εικόνα ενός ομοιομορφισμού που μεταφέρει έναν κύκλο στον τρισδιάστατο χώρο.
Ένας κρίκος με k συνιστώσες είναι η ομοιομορφική εικόνα k κύκλων στον τρισδιάστατο Χώρο. Κάθε κόμβος που απαρτίζει τον κρίκο ονομάζεται συνιστώσα του κρίκου. Ένας κρίκος με μια μόνο συνιστώσα ονομάζεται κόμβος.
Δύο κόμβοι k1, k2 οι οποίοι μπορούν να μετασχηματιστούν ο ένας στον άλλο μέσω μίαςισοτοπίας ονομάζονται ισοτοπικοί.
Μια ισοτοπία είναι μια συνεχής ελαστική παραμόρφωση του Χώρου (δηλαδή ένας ομοιομορφισμός του χώρου) που μεταφέρει τον k1 στον k2.
Κινήσεις Reidemeister[]
Ένα σημαντικό βήμα στη μελέτη των κόμβων ως προς την έννοια της ισοτοπίας είναι η αναπαράσταση των κόμβων από κανονικές προβολές τους στο επίπεδο, που ονομάζονται διαγράμματα.
Ένα διάγραμμα κόμβου σε κάθε διασταύρωση έχει την πληροφορία "άνω" (up) ή "κάτω" (down). Ο Kurt Reidemeister κατάφερε να αποδείξει το 1935 πως οποιαδήποτε ισοτοπική κίνηση ενός κόμβου στο Xώρο μπορεί να επιτευχθεί στο επίπεδο με μόνο τρεις βασικές κινήσεις. Αυτές έγιναν γνωστές ως κινήσεις Reidemeister.
- Η πρώτη κίνηση Reidemeister συμβολίζεται με RI και απλά προσθέτει ή αφαιρεί μια διασταύρωση μέσω μιας απλής αναδίπλωσης.
- Η δεύτερη κίνηση Reidemeister συμβολίζεται με RII και προσθέτει ή αφαιρεί ταυτόχρονα δύο διασταυρώσεις.
- Η τρίτη κίνηση Reidemeister συμβολίζεται με RIII και μας επιτρέπει να μετακινήσουμε ένα τμήμα του κόμβου από τη μια πλευρά μιας διασταύρωσης στην άλλη.
Δύο διαγράμματα κόμβων που διαφέρουν κατά κινήσεις Reidemeister θα λέγονται επίσης ισοτοπικά.
Αναλλοίωτες Κόμβων[]
Είναι πάρα πολύ δύσκολο να αποφανθούμε εάν δυο δεδομένοι κόμβοι είναι ισοτοπικοί ή όχι. Το πρόβλημα της ταξινόμησης των κόμβων αποτελεί ένα ανοικτό πρόβλημα των μαθηματικών.
Έτσι, προσπαθούμε να κατασκευάσουμε αναλλοίωτες, δηλαδή συναρτήσεις από κλάσεις ισοτοπίας κόμβων σε κάποιο σύνολο τιμών (π.χ πολυώνυμα, αριθμοί κ.λ.π.)
Μια αναλλοίωτη είναι ιδιότητα της ισοτοπικής κλάσης ενός κόμβου και όχι ενός διαγράμματός του. Εξ ορισμού μια αναλλοίωτη κόμβων λαμβάνει την ίδια τιμή σε ισοτοπικούς κόμβους.
Ισοδύναμα, αν μια αναλλοίωτη λάβει διαφορετικές τιμές σε δύο κόμβους, τότε αυτοί οι κόμβοι είναι μη ισοτοπικοί και επομένως διαφορετικοί μεταξύ τους. Αυτή ακριβώς η ιδιότητα των αναλλοίωτων βοηθάει στην ταξινόμηση των κόμβων.
Κλασσικές Αναλλοίωτες Κόμβων[]
Υπάρχουν αρκετές κλασσικές αναλλοίωτες κόμβων. Μερικές είναι:
- η τριχρωματισιμότητα,
- ο αριθμός διασταυρώσεων (crossing number),
- ο αριθμός γεφυρών (bridge number) και
- ο αριθμός λύσεως (unknotting number).
Ο αριθμός διασταυρώσεων, ο αριθμός γεφυρών και ο αριθμός λύσεως ορίζονται στο σύνολο όλων των διαγραμμάτων ενός κόμβου.
Τριχρωματισιμότητα[]
Μια κλασσική αναλλοίωτη είναι η τριχρωματισιμότητα. Ένας κόμβος λέγεται τριχρωματίσιμος αν ένα διάγραμμα του μπορεί να χρωματιστεί με τρία διαφορετικά χρώματα έτσι ώστε να ικανοποιούνται τα ακόλουθα:
- Κανόνας 1ος: Σε κάθε διασταύρωση είτε και τα τρία τμήματα του κόμβου έχουν διαφορετικό χρώμα είτε όλα το ίδιο.
- Κανόνας 2ος: Όλα τα χρώματα χρησιμοποιούνται για να χρωματιστεί ο κόμβος.
Aριθμός Διασταυρώσεων[]
O αριθμός διασταυρώσεων (crossing number) ενός κόμβου K, συμβολίζεται με c(K) και είναι ο ελάχιστος αριθμός διασταυρώσεων στο πλήθος όλων των διαγραμμάτων του Κ. Ένα διάγραμμα του K μπορεί να χαρακτηριστεί ως ελάχιστο διάγραμμα εάν και εφόσον έχει μόνο c(K) διασταυρώσεις.
O αριθμός διασταυρώσεων είναι πολύ χρήσιμος στην ταξινόμηση των κόμβων. Πράγματι, ένας κόμβος γενικά ταξινομείται με έναν αριθμό της μορφής CN και αντιπροσωπεύει τον Nιοστό κόμβο με ελάχιστο αριθμό διασταυρώσεων C. Για παράδειγμα ο κόμβος trefoil ταξινομείται ως 31γιατί έχει αριθμό διασταυρώσεων 3.
Αριθμός Γεφυρών[]
Μια γέφυρα σε ένα διάγραμμα ενός κόμβου είναι ένα μέγιστο τμήμα του διαγράμματος, τέτοιο ώστε αν βαδίζει κανείς κατά μήκος του να βρίσκεται συνεχώς "πάνω".
Ο αριθμός γεφυρών (bridge number) ορίζεται παρόμοια με τον αριθμό διασταυρώσεων. Ο αριθμός γεφυρών ενός κόμβου K συμβολίζεται με b(K) και αντιπροσωπεύει τον ελάχιστο αριθμό γεφυρών στο πλήθος όλων των διαγραμμάτων του K.
O αριθμός γεφυρών μιας ισοτοπικής κλάσης διαγραμμάτων δεν διαφαίνεται απαραίτητα από ένα ελάχιστο διάγραμμα της κλάσης. Παράδειγμα, ο αριθμός διασταυρώσεων του κόμβου trefoil είναι 3 και το ελάχιστο διάγραμμα του κόμβου έχει τρεις γέφυρες. Όμως ο αριθμός γεφυρών του κόμβου trefoil είναι 2.
Όταν b(U)=1, τότε ο U είναι ο τετριμμένος κόμβος. Aρα, και όπως έχει αποδειχθεί, για να μην είναι ένας κόμβος K ο τετριμμένος θα πρέπει b(K)>1.
Οι κόμβοι και κρίκοι με 2 γέφυρες έχουν ταξινομηθεί από τον Schubert (1956) και είναι γνωστοί ως ρητοί κόμβοι (2-bridge knots ή rational knots).
Αριθμός Λύσεως[]
Ο αριθμός λύσεως (unknotting number) ενός κόμβου K συμβολίζεται με u(K) και αντιπροσωπεύει τον ελάχιστο αριθμό διασταυρώσεων, στο πλήθος όλων των διαγραμμάτων του K, που πρέπει να αλλάξουν για να δημιουργηθεί ο τετριμμένος κόμβος. Όπως ο αριθμός γεφυρών έτσι και ο αριθμός λύσεως δεν διαφαίνεται απαραίτητα από ένα ελάχιστο διάγραμμα της κλάσης.
Συμβολισμοί Κόμβων[]
Υπάρχουν τρείς συμβολισμοί:
- ο συμβολισμός Dowker,
- ο συμβολισμός Bar Natan και
- ο συμβολισμός Conway.
Επίσης και η θεωρία των "πλεξίδων" (braids theory).
Εφαρμογές[]
Εφαρμογή στην Κοσμολογία[]
Η Θεωρία Κόμβων αναπτύχθηκε αρχικά με σκοπό να εφαρμοσθεί στη Χημεία. Ο λόρδος Kelvin και η Χημεία έδωσαν το έναυσμα για να αναπτυχθεί η Θεωρία Κόμβων τη δεκαετία του 1880. Ο Kelvin υπέθεσε πως όλο το Σύμπαν περιβαλλόταν από μια ουσία, τον αιθέρα, και πως η ύλη μπορούσε να περιγραφεί ως κόμβοι μέσα σε αυτόν. Όμως, όπως γνωρίζουμε σήμερα αυτό δεν είναι αληθές. Αυτό που οδήγησε τη Θεωρία Κόμβων να γίνει ένας σημαντικός κλάδος των μαθηματικών ήταν το πρόσφατο ενδιαφέρον.
Εφαρμογή στην Θεωρία Γραφημάτων[]
Η πρώτη, ίσως, εφαρμογή της Θεωρίας Κόμβων είναι στη Θεωρία Γραφημάτων. Πράγματι, το 1983 οι Conway και Gordon απέδειξαν, χρησιμοποιώντας αναλλοίωτες ισοτοπίας,
- ότι κάθε εμφύτευση του πλήρους γραφήματος Κ6 στο χώρο περιέχει έναν μη τετριμμένο κρίκο και
- ότι κάθε εμφύτευση του πλήρους γραφήματος Κ7 στο χώρο περιέχει έναν μη τετριμμένο κόμβο.
Εφαρμογή στην Στατιστική Μηχανική[]
Με την ανακάλυψη του πολυωνύμου Jones το 1984, ο ίδιος ο Jones ανακάλυψε επίσης θεμελιώδεις σχέσεις ανάμεσα στη Θεωρία Κόμβων και στη Στατιστική Μηχανική. Η Στατιστική Μηχανική μελετά μεγάλα συστήματα μορίων και εξετάζει τη συνολική συμπεριφορά ενός συστήματος ως προς ιδιότητες όπως η θερμοκρασία, η ενέργεια, η αλλαγή φάσεως κ.λ.π.
Πιο συγκεκριμένα, από μοντέλα αλληλλεπιδράσεων γειτονικών μορίων τα οποία θεωρούνται ως κορυφές γραφημάτων, βρίσκεται η συνάρτηση διαμέρισης του συστήματος, η οποία περιέχει τις παραπάνω πληροφορίες για το σύστημα.
Αποδεικνύεται ότι η συνάρτηση διαμέρισης κάποιων μοντέλων σχετίζεται με πολυώνυμα γραφημάτων τα οποία με τη σειρά τους σχετίζονται με αναλλοίωτες κόμβων. Για παράδειγμα το μοντέλο Potts, που εξηγεί την τήξη του πάγου, σχετίζεται με το διχρωματικό πολυώνυμο για γραφήματα, το οποίο οδηγεί στο πολυώνυμο Jones για κόμβους.
Εφαρμογή στην Βιολογία[]
Η Μοριακή Βιολογία μελετά μεταξύ άλλων, το φαινόμενο της αναδιάταξης (recombination) του DNA, κατά το οποίο κάποια ένζυμα, τα τοποϊσόμερα, δρουν στο μόριο, κόβοντας τη διπλή έλικα, και τα τέσσερα ελεύθερα άκρα επανακολλούν με διαφορετικό τρόπο.
Αυτή η δράση των ενζύμων προκαλεί την εμφάνιση κόμβων στο DNA.
Η αναδιάταξη γίνεται σε ελάχιστο χρονικό διάστημα, γι' αυτό οι μοριακοί βιολόγοι αναζητούν ένα θεωρητικό μοντέλο που να περιγράφει την ακριβή διαδικασία της δράσης των ενζύμων. Ένα τέτοιο μοντέλο δόθηκε το 1989 από τους Ernst και Sumners και βασίζεται στη θεωρία των ρητών διαπλοκών και στην ταξινόμηση των ρητών κόμβων, εξηγώντας έτσι επιτυχώς ένα πείραμα πολλαπλής αναδιάταξης.
Εφαρμογή στην Χημεία[]
Η Θεωρία Κόμβων έχει βρει ενδιαφέρουσες εφαρμογές στην κατασκευή μορίων εναντιομερών. Τα εναντιομερή είναι μια ειδική κατηγορία ισομερών, δηλαδή μορίων με τον ίδιο μοριακό τύπο αλλά διαφορετική σύνδεση των ατόμων στο χώρο. Συγκεκριμένα, δύο εναντιομερή είναι το ένα κατοπτρική εικόνα του άλλου. Αυτό συνεπάγεται διαφορετικές φυσικές ιδιότητες των στοιχείων.
Οι χημικοί ενδιαφέρονται ιδιαίτερα να κατασκευάζουν εναντιομερή, προκειμένου να βρίσκονται νέα υλικά με συγκεκριμένες ιδιότητες. Ένας τύπος εναντιομερών, τα τοπολογικά εναντιομερή, είναι μόρια με μορφή κόμβου ή με μορφή κλίμακας Moebius.
Είναι πολύ σημαντικό για τους χημικούς να γνωρίζουν εάν ένα μόριο είναι αμφίχειρο, δηλαδή ισοτοπικό με την κατοπτρική του εικόνα ή όχι. Αν δειχθεί με τοπολογικές μεθόδους ότι ένα μόριο είναι αμφίχειρο, τότε μπορεί να αποφευχθεί η πολυδάπανη και χρονοβόρα διαδικασία κατασκευής του εναντιομερούς του στο εργαστήριο. Για παράδειγμα ο κόμβος figure-8 είναι αμφίχειρος ενώ ο κόμβος trefoil είναι μη αμφίχειρος. Τέτοιες μέθοδοι έχουν δοθεί επιτυχώς από τον J. Simon, την E. Flapan κ.α. (1986, 1987).
Εφαρμογή σην Θεωρία Πολυπτύχων[]
Η Τοπολογία Χαμηλών Διαστάσεων μελετά τρισδιάστατους χώρους (προσανατολίσιμους, συνεκτικούς και συμπαγείς, χωρίς σύνορο) πέρα από τον γνωστό Ευκλείδειο χώρο, που ονομάζονται 3-πολύπτυχα ή 3-πολλαπλότητες (3-manifolds).
Το πρόβλημα της ταξινόμησής τους ως προς τη σχέση του ομοιομορφισμού είναι ένα από τα μεγάλα προβλήματα των μαθηματικών (Εικασία Poincaré).
Κάθε 3-πολλαπλότητα μπορεί να κατασκευαστεί από έναν (τουλάχιστον) κόμβο μέσω της "τοπολογικής χειρουργικής". Επιπλέον, δύο 3-πολλαπλότητες είναι ομοιομορφικοί χώροι αν και μόνον αν οι αντίστοιχοι κόμβοι σχετίζονται μέσω ισοτοπίας και "κινήσεων Kirby". Έτσι, μια αναλλοίωτη ισοτοπίας, αν μπορεί να γίνει αναλλοίωτη και κάτω από τις κινήσεις Kirby, δίνει μια αναλλοίωτη 3-πολλαπλότητων. Επομένως, το πρόβλημα της ταξινόμησης των κόμβων σχετίζεται με το πρόβλημα της ταξινόμησης των 3-πολλαπλοτήτων.
Ειδικά Θέματα[]
Πολυώνυμο Kauffman bracket[]
Ένα παράδειγμα ισοτοπίας είναι το πολυώνυμο Kauffman bracket, το οποίο δίνεται από μία γραμμική σχέση διαγραμμάτων. Αποδεικνύεται ότι είναι αναλλοίωτη ισοτοπίας.
Πλεξίδες[]
Οι κόμβοι σχετίζονται με κάποια άλλα τοπολογικά αντικείμενα, τις πλεξίδες (ή κοτσίδες) (braids).
Το σύνολο των πλεξίδων με n κλωστές έχει δομή αλγεβρικής ομάδας (η ομάδα του Artin). Υπάρχει αλγόριθμος που μετατρέπει κόμβους σε κοτσίδες (Θεώρημα Alexander.
Πολυώνυμο Jones[]
Το 1984 ο V.F.R. Jones κατασκεύασε μία πολύ ισχυρή αναλλοίωτη ισοτοπίας, το πολυώνυμο Jones, χρησιμοποιώντας την θεωρία των αλγεβρών Hecke.
Οι Άλγεβρες Hecke προκύπτουν από "κβαντοποίηση" των συμμετρικών ομάδων.
Θεματολογία[]
- ισοτοπία κόμβων,
- το Θεώρημα Reidemeister,
- κλασσικές αναλλοίωτες κόμβων.
- Η θεμελιώδης ομάδα τοπολογικού χώρου
- η πρώτη ομάδα ομολογίας.
- Η θεμελιώδης ομάδα του κύκλου και
- εφαρμογές στο Θεμελιώδες Θεώρημα Αλγεβρας και στο Θεώρημα Brouwer σταθερού σημείου.
- Η παράσταση Wirtinger για το τοπολογικό συμπλήρωμα κόμβου.
- Το Θεώρημα Van Kampen και εφαρμογή στην κατάταξη επιφανειών και σε θεμελιώδεις ομάδες κόμβων.
- Η επιφάνεια Seifert και το γένος κόμβου.
- Ρητές πεδικλώσεις και η ταξινόμησή τους από τους ρητούς αριθμούς.
- Οι ρητοί κόμβοι, η ταξινόμησή τους
- Θεώρημα Schubert
- εφαρμογή στην αναδιάταξη του DNA.
- Το πολυώνυμο Kauffman bracket,
- το πολυώνυμο Jones,
- το πολυώνυμο Alexander,
- το πολυώνυμο HOMFLYPT:
- . Κόμβοι και επίπεδα γραφήματα,
- η ηλεκτρική αγωγιμότητα,
- σύνδεση με Στατιστική Μηχανική.
- Κόμβοι και εμφυτευμένα γραφήματα
- Θεώρημα Conway-Gordon,
- εφαρμογές σε πολυμερή.
- Κόμβοι και κοτσίδες,
- Θεώρημα Alexander
- Θεώρημα Markov,
- Άλγεβρα Hecke και
- το ίχνος Ocneanu.
- Κατασκευή τρισδιάστατων πολλαπλοτήτων με χειρουργική σε κόμβους.
- Η αναλλοίωτη Witten (κατά Lickorish) τρισδιάστατων πολλαπλοτήτων.
Εσωτερική Αρθρογραφία[]
Βιβλιογραφία[]
1) C.C. Adams, “The Knot Book”, Freeman.
2) A. Hatcher, “Algebraic Topology”, Cambridge.
3) D. Rolfsen, “Knots and Links”, Publish or Perish.
4) W.B.R. Lickorish, “An Introduction to Knot Theory”, Springer.
5) L.H. Kauffman, “Knots and Physics”, World Scientific.
6) L.H. Kauffman and S. Lambropoulou, The classification of rational knots, L’ Enseignement Mathématique, 49, 2003.
7) D.W. Sumners, Untangling DNA, Mathematical Intelligencer, 12(3), 1990.
8) J.H. Conway and C.McA. Gordon, Knots and links in spatial graphs, J. Graph Theory, 1983.
9) S. Lambropoulou and C.P. Rourke, Markov's theorem in 3-manifolds, Topology and its Applications, 78, 1997.
10) V.F.R. Jones, Hecke algebra representations of braid groups and link polynomials, Annals of Mathematics, 126, 1987.
Ιστογραφία[]
- math.ntua.gr
- Ομώνυμο άρθρο στην Βικιπαίδεια
- Ομώνυμο άρθρο στην Livepedia
- math.ntua.gr
- Torus knots as Hopfions
|
Αν και θα βρείτε εξακριβωμένες πληροφορίες "Οι πληροφορίες αυτές μπορεί πρόσφατα Πρέπει να λάβετε υπ' όψη ότι Επίσης, |
- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν
- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)
